Now what happens if we change the parameters of amplitude of the forcing function and/or the rate of energy loss. This in effect gives us a whole new dynamical system that must be explored. So we distinguish between changing the system and changing the initial conditions of the system. The next display is for a system that has quite a different sort of attractor. For the chosen values of amplitude and drag there is a single attractor which is a "chaotic", or a "strange" attractor.

Notice the irregularity of the Position/Velocity vs. Time view in the next display. This fellow spends some time on the plus side of the origin and some on the minus, and remains in the general vicinity, so he meets our definition of an oscillator. However, as you scan out along the time axis by repeated clicks on Action, you will not find any true periodicity. In fact, pick any state, a set of values for x and x', and that exact state will not be repeated, if you watched forever. Run the DMO Chaotic Attractor display, P and V vs. Time view and come on back here so we can talk about it.

The kind of unrepeatability you saw in this system is a tough thing for those of us in the future predicting business. When a system breaks into this chaotic behavior we are in big trouble as far as saying in detail what the future state will be even in the short term. Before we go on to look at the other views of this system, run the DMO Sensitivity to Initial Conditions display.

The significance of sensitive dependence on initial conditions is that the divergence in system behavior grows exponentially in time. This means that for a dynamical system whose attractor is chaotic, if the conditions are disturbed by the slightest amount, the behavior from that point on will begin to diverge such that after a time it will have no relationship to what it would have been in the absence of that disturbance.

With regard to the world's weather, this idea of sensitive dependence to initial conditions has been called the butterfly effect. The premise is that the beating of a butterfly's wings in Canada might result later in a typhoon in the Philippines. This of course supposes that the world's weather as a dynamical system is operating in a mode where it is on a chaotic attractor. That remains to be conclusively demonstrated but it sure looks chaotic. What if the world itself as a dynamical system has a chaotic history? It does not bode well for time travel.

Given the wild behavior we have seen, is there anything we can say about the future of a dynamical system in chaos. Well, of course there is or we would not be wasting our time with it. Let's go back to the DMO Chaotic Attractor display and look at the Phase Space Projection view. Let it run a few seconds just to a sense of the shape of the projection on the (x,x') plane. Then we can talk about it.

The key to analyzing systems in chaos is to remember that a chaotic attractor is still an attractor. When we disturbed dynamical systems that were on their attractor, be it a point attractor or a periodic attractor, the state point in phase space temporarily wandered off but after the transient died away they returned to the attractor. When the attractor is chaotic the same effect is seen. The difference is that the instantaneous value of the state variables at any time after the disturbance, bears no predictable resemblance to the values that would have pertained in the absence of the disturbance except that we know that they both will lie on the attractor somewhere.

By observing the Phase Space Projection view of the system attractor, we can begin to make some predictions. At least in the time you let the plot develop, there seems to be certain values of x and x' which are excluded from the attractor. if you like, go back and let it run longer here, to see if after more time passes the overall dimensions of the plot change or if there are any wild excursions into previously uncharted states.

You should be gaining some comfort at this point that at least for this system, the attractor inhabits a well-defined region of the phase space. Also you might be curious about the odd shape the return point markers seen to be making. They are sort of smeared up and down in the x'dimension on the plus side of the x-axis. More about that later. Now take a look at the Chaotic Attractor display in the Phase Space Orbit view. Yaw and pitch it around awhile to begin to get some sense of the general shape. Remember that no two states are the same in the whole bundle of orbit strands, no matter how long you let it run.

The idea of confining a line of infinite length in a finite volume and requiring that it never cross itself might give us some trouble in visualizing the situation. Hopefully the displays so far have helped. The phase space orbit is like a skein of yarn where each strand is infinitely fine. The attractor is the region of phase space where these strands tend to accumulate. If I disturb the system in some way, displacing a strand from the attractor, time will bring it back to that certain region. Thus the term "attractor" is justified.

When we were dealing with periodic attractors, the phase space orbit was a few well-defined loops. Here the attractor instead of being a finite number of loops as it was for the periodic attractors, is an infinite bundle of loops in the vicinity of the time axis circle. These loops are a hopeless tangle but we know they never intersect each other. If they did the conditions at the intersection would be identical so that future development would also be identical to the past, making the system repeat perhaps with a very large periodicity. In fact is was only recently in the history of mathematics that people became aware that there was a distinction between a periodic attractor with very long period and a chaotic attractor.

What is not obvious from the Phase Space Orbit view is that the bundle of loops in the orbit has an intricate structure of its own. The region in phase space occupied by the orbit is not just a badly formed bagel as it appears from pitch and yaw at (90,0) or a doorknob, as it appears from pitch and yaw at (0,0). If we slice through the orbit at a series of (x,x') planes spaced around the time axis circle, we will see that the cross sections have an intricate shape. 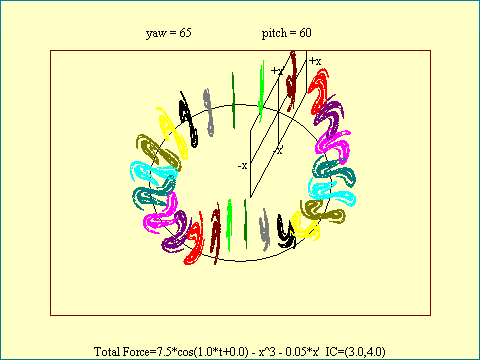The Orbit Sections view is where that structure becomes visible. Run the model in the Orbit Sections view after setting the pitch to 60 degrees and the yaw to 65 degrees to see this. Go ahead and do this now. Allow quite a bit of time for this view to develop.

The Orbit Section view suppresses the orbit plot between sectioning planes and illuminates the pixels where the orbit hits the planes in a succession of colors so as to make the cross section details visible. What we see now is that the attractor does not occupy all the phase space included in the bundle of orbit loops. Rather it apparently exists in convoluted layers. The Poincaré Section view takes one of these cross sections and expands it for a more detailed look at this internal structure. Run the model again in that view. Since we have to integrate a full orbit loop to get a single pixel lit, this view takes time to develop.

This is probably a good point to remind you that the fantastic images we are looking at arise from the behavior of a real mechanical system. These images take on a life of their own and I tend to get fascinated by the images themselves. The object of all this though is to be able to make at least some predictions about the future of a real system.

The structure revealed in the Poincaré section of our attractor looks like the layers one might see in pastry dough which had been repeatedly folded and rolled. In fact if we took a bundle of orbit strands which initially ran parallel and stretched the bundle out into a thin band, then folded the band back on itself, repeating the process a few times we would find the result would look much like the skein of strands we see in our chaotic orbit. Strands initially close together would now be far apart and vice versa. This stretching, folding and flattening has a mixing effect that is the origin of the sensitivity to initial conditions we observed earlier.

The Poincaré section of the chaotic attractor reveals the details of the attractor's structure. You should have noticed that there were areas where the orbit strands accumulated and areas where the strands never went. This boundary between light and dark in the Poincaré section is irregular in the extreme. This sort of wild border region between certain domains is a recurring theme in the mathematics of chaos. Examination of highly irregular boundaries such as we see here is a matter of great interest. So irregular is this boundary that any section of the (x,x') plane that contains a strand of the orbit will also contain part of the boundary, however small that section may be.

The question, "How long is the coast of Maine?" is not easily answered. If you measure the Maine coastline with a yardstick you would miss a lot of tiny coves and inlets less than three feet across. A one-foot ruler would measure more precisely than a yardstick. A one-centimeter ruler more precisely than a one-foot rule. The length of the Maine coast depends on the length of your ruler and in the limit as the ruler length approaches zero, the coast length becomes extremely long almost infinite. Likewise the boundary of the Poincaré section of the chaotic attractor we have plotted. The closer you look, the more detail is revealed.

A slice through the chaotic attractor for Duffing's mechanical oscillator then has a boundary that is infinite in length but contained in a finite region of the (x,x') plane. Regions of space which have an infinite boundary but finite extent are called "fractals". We are accustomed to think of a line as being of one dimension and a plane as being of two dimensions. A fractal boundary is more than a line but less than a plane and sure enough it has dimension between one and two. A fractional dimension. Very strange. The fractional dimension and fractured nature give rise to the name fractal.

Of course as we continue to zoom in, we still need to calculate the orbit loops that never penetrate our section of the (x,x') plane so the time to illuminate a certain number of pixels in the image goes up dramatically as the size of the viewing window decreases. This limitation is inherent in mathematical modeling. If it were possible to get an analytical expression for the solution to the model differential equation we could jump in with any value of time and immediately calculate the state. This sort of random access is one of the benefits of the explicit solution.

The fact is with motions as complicated as we have uncovered here, there is no solution available so we must go chronon by chronon in a serial fashion to any point we want to see. It is small wonder that this kind of analysis had to wait for the computer to be invented. Forty years ago people would have had to work for a lifetime to get 0.1% of the information you have seen in the last few minutes.

Suppose now we had a stream of data from some dynamical system which appeared to jump around erratically, without order. If we could plot a Poincaré section of that data and it revealed a cross section we could recognize as a fractal, we would know that we were not dealing with random data but with a dynamical system on a chaotic attractor. That would be a piece of future prediction worth having.

The one remaining view is the Basins of Attraction. Since we have only one attractor for this dynamical system, it is not of much use here. You may run the view to see what path any particular set of starting conditions takes to reach the attractor if that is of interest to you. In the full powered (offline) version of this program, you may actually map the basins of attraction of the periodic attractors we studied earlier, as shown at the right.

The last lesson in this section on dynamical systems is a research lab where you will be able to set the parameters that define a Duffing mechanical oscillator and explore it for attractors. I will provide several examples but after that you are on your own.

Are there any questions?