Systems of many particles

The work of a curious fellow

E pluribus unum - or e unus pluribum, it could go either way...

So far we have mostly been dealing with one particle at a time. Remember that a particle is an object whose own dimensions may be neglected in the system under study. Now I want to begin talking about objects that have some noticeable size. Just as we dealt with the area under a curve by slicing it into thin slabs, we may deal with objects of finite extent by considering them to be made up of very many pieces, each small enough to be considered a particle.

In our previous work it was time and distance that we looked at in small bits called dt and dx. Now it will be mass as well that we want to subdivide. In fact there is convincing evidence that chunks of matter really are made up of tiny pieces, smaller than which nothing is. These tiny pieces individually exhibit particle behavior. It is not clear that time and distance have any minimum sized quantities but it is interesting to think about the possibility. How would we know if time, for example were discontinuous?

In considering the motion of a particle (how its position depends on time) we discovered that we were able to look at it one dimension at a time so as to avoid a lot of vector arithmetic. In that way there are three equations of motion to totally specify the movement of a free particle in space. How many equations of motion would it take to specify the motion of two particles? Right...three apiece or six. And a thousand particles? Yup, three thousand equations of motion involving acceleration, velocity and position. So for a 56-kilogram lump of iron, having 6.02e26 iron atoms in it, to specify its motion one atom at a time would be quite inconvenient.

To get out of the mess implied in the preceding paragraph we use a trick we have used before, even though I did not mention it specifically at the time. When we talked about the block and spring apparatus we described a particle that was constrained by the rails upon which it was sliding. Since it could not move in any direction but plus and minus x, the number of equations required to completely specify the motion was one.

By applying the constraint of the rails, we reduced the number of equations needed to specify the motion. In general we will look to use "constraints", physical properties of a system that reduce the number of "degrees of freedom" the system has. Degrees of freedom are the number of independent variables required to completely specify the position of an object. Each independent variable brings with it the need for an equation of motion to specify the motion, so the application of appropriate constraints can greatly simplify the arithmetic.

Getting back to our lump of iron with a zillion atoms in it. If we had to treat each atom without constraint, we would have to solve at least 3 zillion equations of motion. Fortunately under the conditions we are interested in right now, iron is a solid. In considering the motion of the lump as a whole, we may apply a constraint that the distance between atoms is fixed. If that is the case, how many degrees of freedom does a lump of iron have? To answer that question we need to figure out how many independent variables are required to specify its position. We suspect that it will be less than three zillion, but is it just three, as was the case for a single particle?

To help you visualize the situation, we will begin with a very simple lump of iron with only two atoms in it. We could specify its motion by independently specifying the change of position of each of the two atoms with respect to time. That would require six variables, an x, y and z for each atom. As an alternative we could specify the position of one atom by x, y and z, then fix the position of the other by giving a direction and a distance from the first. But here is where the beauty of the constraint comes in.

In predicting the future of this two-atom lump of iron, we are only interested in parameters which may be different in the future than they were in the past. Since the distance between the atoms is constant, we may ignore the distance in specifying changes in position. So I can completely specify the motion by a set of five numbers, the x, y and z coordinates of one atom and the distance of the other atom from any pair of axes. Run the Two Atom Lump display to see what I mean.

Now suppose I add a third atom to the lump, having tied down two original atoms by specifying the five numbers. Is it possible to have any motion of the system? If it is, then the addition of the third atom introduced additional freedom to the system. Run the Three Atom Lump display to check this out.

Clearly the third atom is not locked in place by the five numbers we specified to hold the two-atom lump fixed in space. Another degree of freedom is evident. How many additional coordinates are required to specify the position of the three atom lump? Well the original five numbers fixed the position of the two atoms and the line joining them. Since the distance of the third atom from the other two is fixed, the only thing we need to know in addition to the original numbers is the orientation of the third atom around the line joining the first two. In the absence of this information we could rotate the third atom around the line joining the first two as shown in the display.

Imagine fixing this orientation by specifying the distance between the third atom and the axis not used in locking up the position of the second atom. As you can see in the display, fixing that would lock up the third atom so a three atom lump has six degrees of freedom, requiring six numbers to specify its position completely. Or in other words six constraints other than the inherent fixed distance, "solid" constraint prevent all motion.

How about a four-atom lump. The distance of the fourth atom from each of the other three is fixed by the solid constraint. In three dimensional space, as long as a particle has three independent constraints, its position is determined. The fourth atom gets three constraints from the solid condition and the three other atoms. Run the Four Atom Lump display to help you picture this condition.

In the four-atom lump you have six constraints, the three coordinates of the red atom at the origin and the three fixed distances to the axes represented by the gray lines. There was nothing special about the particular fourth atom we chose to include so the position of any atom in the lump, even if there are zillions, is determined by only six numbers. In other words solid objects, otherwise unconstrained have six degrees of freedom. So in the most general case we can specify the future of any solid object with only six equations of motion. That is quite a bargain considering the number of particle that make up most solids.

Still six equations might be hard to work with. We need some way to organize them into manageable groups. Since we have already done a lot of work with the motion of a particle, wouldn't it be nice to be able to apply those ideas to objects of finite extent? Well of course it would, otherwise I would not have brought it up. So we shall proceed a ways in that direction.

In looking at the degrees of freedom of our lumps, you may have noticed that there were essentially two kinds of freedom. One sort of freedom was freedom for the atoms to move all together without changing their relative position to each other. We will call that kind of motion "translational" motion or translation. In translational motion each point in a body experiences the same displacement as any other point as time goes on, so that the motion of one particle represents the motion of the whole body.

The other kind of freedom we saw in our iron lumps was the freedom for the atoms to move relative to each other without the whole lump partaking in the motion. In our examples so far this sort of freedom involved rotation of one or more of the atoms. There is another possibility for this sort of non-translational motion if the solid constraint is somewhat less than solid so that atoms may average some fixed distance from each other but vibrate about this average position. This in fact is the nature of solids if you look at fine enough detail. For now however we will ignore the tiny vibrations of individual atoms and focus on bulk motion of the object. The familiar airborne object in the image at the left illustrates the two types of motion.

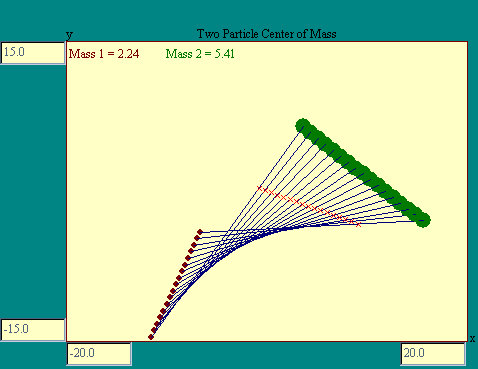
Even when an object vibrates or rotates as it moves, there is point in the body, called the "center of mass", that moves in the same way that a single particle subject to the same external forces would move. To get at this center of mass idea consider a two particle system with masses m₁ and m₂ for the particles. Let particle 1 be located at x₁ on the x axis of our reference frame and particle 2 be located at x₂. The center of mass is defined as a point x_cm = (m₁ * x₁ + m₂ * x₂) / (m₁ + m₂).

The center of mass lies on the line joining the two masses and somewhere between them. If either m₁ of m₂ is zero, you can see that the center of mass just moves to the location of the other particle. Run the Two Particle Center of Mass display for an illustration.

To extend this definition to more than two particles in a straight line, x_cm = (m₁ * x₁ + m₂ * x₂ +...+ m_n * x_n) / (m₁ + m₂ +...+ m_n). In this formula n represents the number of particles and the expressions in parentheses represents the summation of all the terms 1 through n. To express this more compactly we could write x_cm = sigma

m_i*x_i /

m_i

Arrrgh! I know I said we would not get too mathematical and this looks like unnecessary symbolism, but you will see this upper case Greek letter sigma used this way in many places. The sigma symbol is interpreted to be the sum of all the terms which follow it where the i in the first term is replaced by 1, in the second term by 2, and so on until in the last term the i is replaced by the number represented by n. The i in these expressions is called a summation index.

The total mass m of all the particles is sigma m_i so m * x_cm = sigma m_i * x_i. Now for a collection of particles not all in one line along the x-axis we can define a center of mass in this way. The center of mass is at (x_cm, y_cm, z_cm) where x_cm = 1/m * sigma m_i * x_i, y_cm = 1/m * sigma m_i * y_i and finally, z_cm = 1/m * sigma m_i * z_i. This may be a good point to remember that when we deal with positions in space we may use either the coordinates x, y and z or we may use a vector to designate a position. Rather than use the generic v for vector, since we are dealing with a position relative to the origin of our reference frame, we will use the symbol r (for radius) as a position vector. In vector notation the center of mass is at r_cm = 1/m * sigma m_i * r_i.

To illustrate the center of mass concept when the particles are not all in a straight line run the Many Particle Center of Mass display.

Notice that there does not need to be any particle at the center of mass, in fact the center of mass does not even have to be inside a solid object. One way to judge the location of the center of mass is to recognize that for solid objects it will be the balance point. An object supported at its center of mass would not tip one way or another. Try laying out the particles in the display to try to find the center of mass of a fishhook shaped object.

Now that we have the center of mass idea firmly in hand let's look at the physical significance of the concept. Consider the equation m * r_cm = m₁*r₁ + m₂*r₂...+ m_n*r_n.

devilish hard This equation holds true now and always. You can find no instant in time when it is not true. Since this is so, we know that the rate of change with respect to time of the left side of our equation is equal to the rate of change with respect to time of the right side. Let's use the ' symbol to represent the rate of change with respect to time of a quantity. For example r' is Dr / Dt. For now considering the mass m to be independent of time so we have m * r_cm' = m₁*r₁' + m₂*r₂'...+ m_n*r_n'. The rate of change equation we just wrote is also true for all time so we can set equal the rate of change of each side of this equation as well so that m * r_cm'' = m₁*r₁'' + m₂*r₂''...+ m_n*r_n'' Remember that r'' is the acceleration of an object located by the vector r, so the equation above says that the total mass times the acceleration of the center of mass is equal to the sum of each particle's mass times its acceleration. The product of each particle's mass times its acceleration, from Newton's second law, is the force acting on that particle. So we arrive at the statement that the total mass of a group of particles times the acceleration of the center of mass is equal to the vector sum of all the forces acting on the group of particles. So m * r_cm'' = f₁ + f₂...+ f_n. Among all the forces acting on the particles will be the internal forces the particles exert on one another. Newton's third law, (remember the action and reaction story), says that all these internal forces act in pairs, action and reaction, so they cancel each other out in the vector sum. The net effect then on the right side of the equation above is the sum of the external or applied forces, f_a. That brings us to the relationship m * r_cm'' = f_a . In words, the center of mass of a system of particles moves as though all the mass were concentrated at that point and all the external forces were applied at that point.

We came to this understanding without saying anything specific about the nature of the system of particles so our result applies to rigid objects in which the particles are at fixed distances from each other, but also any collection of particles even if there is very complicated internal motion relative to the center of mass. By introducing the center of mass idea, we got to the fact that in systems of many particles, the center of mass moves exactly like a single particle so we can adopt the whole set of results already developed for one particle to describe the translational motion of the whole system.

In the next lesson we will extend our understanding of translational motion.

Are there any questions?

Other