The lessons in this course are organized around a series of illustrations. The text describes what the image is intended to convey. Included in the text you will find links to the interactive displays from which the images were taken. This arrangement allows the pages to be rendered on the screen rather quickly, with the gist of the story intact. It is the interactive displays though, that make this online material different than a printed text. I urge you to take the time to follow each link on the pages and play around with the displays. It is there that much of the learning takes place. At the bottom of each page, with the site navigation links, is a link to a glossary to help with unfamiliar terms.

In due course we will discover exactly what the image at the left is and how it was made. This image was actually created in an interactive display that comes up in the offfline version of the Order course. The online version has its limitations.

Let's begin this journey together more or less at the beginning with a quick review of numbers and arithmetic. Certain numbers are called "real", which seems to mean that there are others, possibly unreal. Real numbers may be thought of as lying along a straight line with zero in the middle and extending as far as imaginable to the right for positive numbers and as far as imaginable to the left for negative numbers. Included are whole numbers (integers), fractions (rational numbers) and decimals not expressible as fractions (irrational numbers).

The image at the right illustrates a short segment of the real number line, between -20 and +20. The indicated example here is an irrational number. Click on the link for the Real Number Line interactive display from which this example was taken.

Real numbers may be added, subtracted, multiplied and divided in the ordinary way. In this program we will use the following symbols for mathematical operations. For addition +, for subtraction - , for multiplication *, and for division /. Raising numbers to powers, sometimes called exponentiation, we place the exponent above the number and to the right, like 3⁴, or we use the ^ symbol like 3^4. Both mean 3 multiplied by itself 4 times. Numbers may be raised to non-integer powers like 2.7^0.5. This is the square root of 2.7. Applying any combination of addition, subtraction, multiplication and division to real numbers results in another real number. Raising real numbers to powers also gives a real result in many cases. We will cover the interesting exception later.

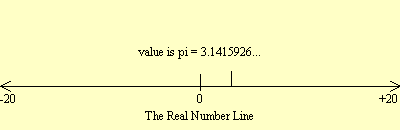
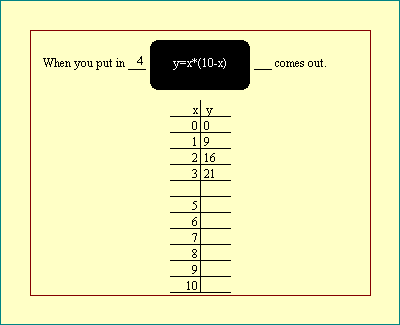
Sometimes mathematicians like to make up rules that produce one number from another, like take a real number and divide it by two to get another real number. Or take a number, multiply it by itself and add a second number to it to get another number. The possibilities are nearly endless. In this program we will deal with some of these rules for combining numbers which in themselves are fairly simple but which under the conditions we will explore, produce wonderfully complicated results. Don't worry, the complications are wonderful but not fearful.

This making up of rules is more than a means of filling the idle hours. It turns out that many physical phenomena may be described by rules like this. Rules of the sort we cover here are called "functions". The number produced is said to be a function of the number "taken" at the beginning. In particular these are called a single valued functions. Each number in, gives one number out. The "taken" number is called the "independent variable" the produced number the "dependent variable". We talk about a function as "returning" the dependent variable.

Frequently the independent variable is called "x" and the dependent variable called "y". We will refer to x and y in that in the rest of this discussion. Some functions have restrictions on the allowed values of x. The set of all values of x which are allowed for the function is called the "domain" of the function. The set of all values of y which the function returns is called the "range" of the function. The word "set" as we will use it just means a collection of related objects or numbers. The mathematical definition is very close to ordinary usage.

In addition to the arithmetic operations of addition, subtraction, multiplication, division and exponentiation; there are other defined functions that operate on real numbers. In particular there are two, which we will use in our examples later. The sine function, symbolized as

Sometimes it is useful to look at the way that y depends on x by plotting the relationship on a graph. We plot the x value along the horizontal direction, called the "x-axis". For each value of x the corresponding value of y is plotted over x in the vertical direction, called the "y-axis". The series of y locations traces out a curve which represents the function. Recognize that any graph represents only a sampling of points covered by the function. It is an accurate representation of the function only if the function has no bizarre behavior between sample points.

On the Graphing display we will demonstrate how a function may be represented by a graph.

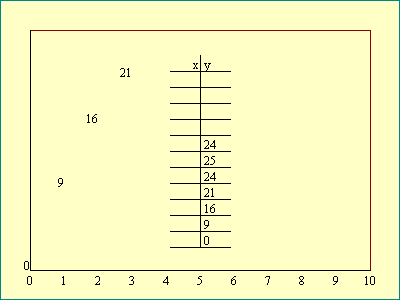
For purposes of introducing the graphing concept, marking the y values with the actual number was OK, but as a practical matter we will not want our graphing illustrations peppered with numbers. We could replace the y numbers with some more convenient marker and move the values to the y-axis as we did with the x values. If this were a paper graph that is what we would do. Then to determine the x and y values called "coordinates" of any point on our graph we would have to estimate the values from the axis scale.

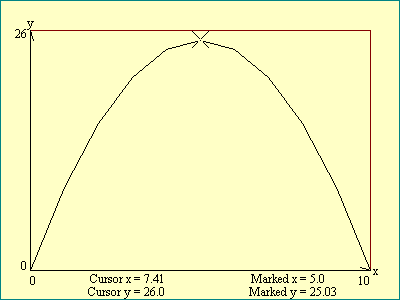
Fortunately we are going to work with computer graphs rather than paper ones. On the computer screen we will take advantage of the cursor provided to us by our operating system. The coordinates of the point on our graph pointed to by the cursor can be displayed and updated as the cursor is moved. The x and y values are displayed in the bottom margin.

Run the Cursor Action display to see the rudimentary graph produced in the Graphing display replaced with a better version.

We draw graphs by selecting a few points along the x-axis, calculate the corresponding y values, plot those points and then connect the dots to fill in all the other uncalculated points representing the function. What we assume in doing this is that the function is fairly smooth and behaves on a small scale pretty much the same way it does on the larger scale covered by the points which were calculated.

There are three functions that we will use later to demonstrate some fundamental principles in this program. There are many which could be used but these meet the requirements and are not too complicated. One is called a quadratic function. It is spoken: y equals gain times x times, 1 minus x. In symbols understandable to computers and programmers it is written:

The symbols x and y are the independent and dependent variables as we mentioned previously. The parameter g which we identified earlier as a coefficient, is just a multiplier. We use the symbol g and call it the "gain" because the action of this parameter on the function is similar to that of the term known as gain in electronic circuits. Rather small variations in the gain will produce radically different behavior of the function under certain conditions as we will see. This particular function is prominent in the mathematics of chaos.

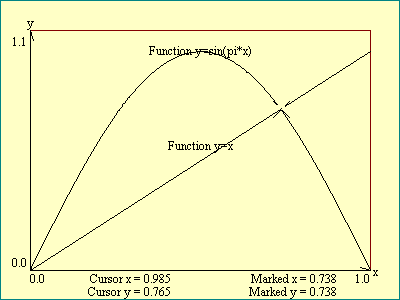
Another function we use is called sinusoidal. It is spoken: y equals gain times the sine of pi times x Written it is:

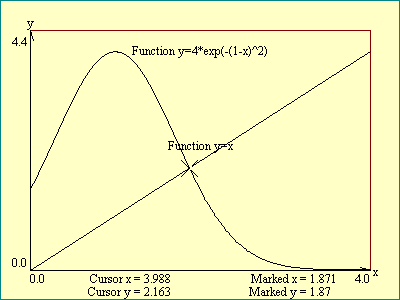
The last function is a little more complicated in form but is commonly used in statistics and all sciences. The name is the Gaussian function, after Mr. Gauss no doubt. It is the famous bell shaped curve that describes the statistical distribution of just about everything. This one is said: y equals g times e to the minus, x minus 1, squared. In symbols:

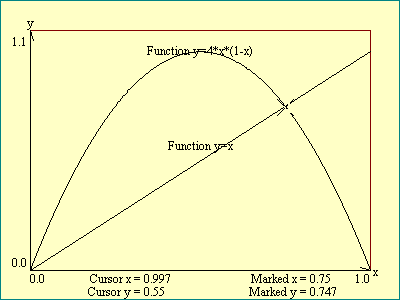
You may show the three functions in turn, in the next display. The functions equation will be displayed along with the graph. The parameter g is set to a value of 4.0 in quadratic and Gaussian examples and to 1.0 in the sinusoidal case. We will have an opportunity to vary it later. The graph displayed is drawn as a continuous line as we discussed. It is the curve we think we would get if we took every possible value of x between our chosen limits, calculated the corresponding y and plotted the points. In fact the computer plots it by dividing the display area into steps whose number is equal to the number of pixels in the width of the drawing area and plotting that many points.

Also plotted on the graph with the selected function is a straight line representing the set of all points on the graph where y=x . It is included here to demonstrate the fact that two independent functions may be displayed on the same graph and to show one way to find the points on the graph which fulfill the conditions of both functions. Use the cursor to find approximately the x and y values where the selected function and the function y=x both hold true. We say these points satisfy the simultaneous equations represented by the two graphs. Play around with these function graphs.

This concludes the Numbers, Functions and Graphs discussion. The next topic is called Extending Graphing Concepts. To view this lesson click on the Next link below.

Are there any questions?